Logic Micro Operations

Logic micro operations specify binary operations for strings of bits stored in registers. These operations consider each bit of the register separately and treat them as binary variables. For example, the OR micro operation with the contents of two registers R 1 and R2 is represented by the statement

P: R1 <- R1 V R2

It specifies a logic microoperation to be executed on the individual bits of the registers provided that the control variable P = 1. As a numerical example, assume that each register has four bits. Let the content of R1 be 1010 and the content of R2 be 1100. The OR microoperation stated above symbolizes the following logic computation:

1010 Content of R1 

1100 Content of R2 

1110 Content of R1 after P = 1  

The content of R1, after the execution of the microoperation, is equal to the bit-by-bit OR operation on pairs of bits in R2 and previous values of Rl.

List of Logic Micro operations

Truth Table for micro operations

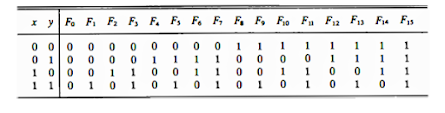
There are 16 different logic operations that can be performed with two binary variables. They can be determined from all possible truth tables obtained with two binary variables as shown in below table. In this table, each of the 16 columns F0 through F15 represents a truth table of one possible Boolean function for the two variables x and y.

List of  Micro Operations

Hardware Implementation

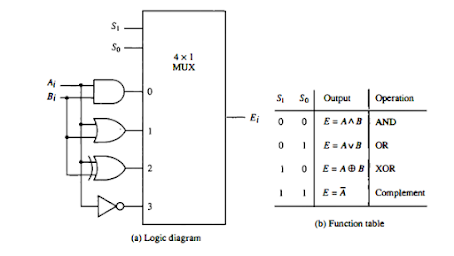
To perform the required logic function the hardware implementation of logic rnicrooperations requires that logic gates be inserted for each bit or pair of bits in the registers. There are 16 micro operations but most of the computers implement only four-AND, OR, XOR (exclusive-OR), and complement from which all others can be derived.

One stage of logic circuit that generates the four basic logic rnicrooperations . It consists of four gates and a multiplexer.The output of the gate is connected to the input of the multiplexer.The two selector lines S1 and S0 choose one of the data inputs and gives it has output of the multiplexer.

one stage of logic circuit

Some Applications 

Logic micro operations are very useful for manipulating individual bits or a portion of a word stored in a register. They can be used to change bit values, delete a group of bits, or insert new bit values into a register

Selective-Set:

The selective-set operation sets to 1 the bits in register A where there are corresponding 1's in register B. It does not affect bit positions that have 0's in B. The following numerical example clarifies this operation: 

1010 A before 

1100 B (logic operand) 

1110 A after 

Selective-Complement: 

The selective-complement operation complements bits in A where there are corresponding l's in B. It does not affect bit positions that have 0's in B. For example:

1010 A before 

1100 B (logic operand)

0110 A after 

Selective-Clear:

The selective-clear operation clears to 0 the bits in A only where there are corresponding 1's in B. For example: 

1010 A before 

1100 B (logic operand) 

0010 A after

Mask:

The mask operation is similar to the selective-clear operation except that the bits of A are cleared only where there are corresponding 0' sin B. The mask operation is an AND micro operation as seen from the following numerical example:

1010 A before 

1100 B (logic operand) 

1000 A after masking 

Insert:

The insert operation inserts a new value into a group of bits. This is done by first masking the bits and then ORing them with the required value. For example, suppose that an A register contains eight bits, 0110 1010. To replace the four leftmost bits by the value 1001 we first mask the four unwanted bits:

0110 1010  A before 

0000 1111  B (mask) 

0000 1010 A after masking

and then insert the new value:

0000 1010  A before

1001 0000  B (insert)

1001 1010  A after insertion