Multivalued Dependencies in DBMS

 

• Multivalued dependency occurs when two attributes in a table are independent of each other but, both depend on a third attribute.
• A multivalued dependency consists of at least two attributes that are dependent on a third attribute that's why it always requires at least three attributes

1. Functional dependencies rule out certain tuples from appearing in a relation.

   If A B, then we cannot have two tuples with the same A value but different B values.

2. Multivalued dependencies do not rule out the existence of certain tuples.

   Instead, they require that other tuples of a certain form be present in the relation.

3. Let R be a relation schema, and let and .

   The multivalued dependency

   

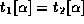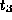   holds on R if in any legal relation r(R), for all pairs of tuples and in r such that , there exist tuples and in r such that:

 

Theory of Multivalued Dependencies

1. We will need to compute all the multivalued dependencies that are logically implied by a given set of multivalued dependencies.
   • Let D denote a set of functional and multivalued dependencies.
   • The closure 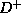of D is the set of all functional and multivalued dependencies logically implied by D.
   • We can compute 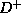from D using the formal definitions, but it is easier to use a set of inference rules.
2. The following set of inference rules is sound and complete. The first three rules are Armstrong's axioms from Chapter 5.
   1. Reflexivity rule: if is a set of attributes and , then holds.
   2. Augmentation rule: if holds, and is a set of attributes, then holds.
   3. Transitivity rule: if holds, and holds, then holds.
   4. Complementation rule: if holds, then holds.
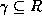   5. Multivalued augmentation rule: if holds, and and 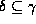, then holds.
   6. Multivalued transitivity rule: if holds, and holds, then holds.
   7. Replication rule: if holds, then .
   8. Coalescence rule: if holds, and , and there is a such that and and , then holds.
3. An example of multivalued transitivity rule is as follows. and . Thus we have , where .

   An example of coalescence rule is as follows. If we have , and , then we have .

4. Let's do an example:
   • Let R=(A,B,C,G,H,I) be a relation schema.
   • Suppose holds.
   • The definition of multivalued dependencies implies that if 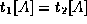, then there exists tuples 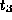and such that:

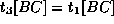
   • The complementation rule states that if then .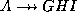
   • Tuples 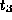and satisfy 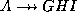if we simply change the subscripts.
5. We can simplify calculating 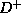, the closure of D by using the following rules, derivable from the previous ones:
   • Multivalued union rule: if holds and holds, then holds.
   • Intersection rule: if holds and holds, then 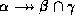holds.
   • Difference rule: if holds and holds, then holds and holds.
6. An example will help:

   Let R=(A,B,C,G,H,I) with the set of dependencies:

   We list some members of :

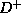   • : since , complementation rule implies that , and R - B - A = CGHI.
   • : Since and , multivalued transitivity rule implies that .

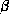   • : coalescence rule can be applied. holds, and and , so we can satisfy the coalescence rule with being B, being HI, being CG, and being H. We conclude that .

   • : now we know that and . By the difference rule, .